Per scommetere in maniera produttiva abbiamo bisogno di due informazioni: la probabilità di vittoria e il possibile guadagno.
Perchè? Prendiamo un caso molto semplice di scommesse a quota fissa. Immaginiamo di avere una moneta non truccata. Le probabilità che esca testa o croce sono esattamente le stesse:0.5. Adesso immaginiamo che la vittoria ci venga pagata a 2, ovvero viene pagato due volte lo stake. Una probabilità di 0.5
significa che su 100 lanci vinceremo circa 50 volte e perderemo circa 50 volte. Immaginiamo di puntare a ogni lancio 1 euro. Quindi su cento lanci
avremo una vittoria netta di 50 euro. Tuttavia perdermo circa le restanti 50 volte. Quindi al netto avremo 0 euro di guadagno. Questa è una fair bet. Ovvero nessuno vince o perde denaro sul lungo periodo. Ora immaginiamo invece che il bookmaker come abbiamo detto nel post precedente lasci che siano
i giocatori a determinare le quote, in base al meccanismo spiegato. Immaginiamo quindi adesso di avere le quote così suddivise:1.9 testa e 2.1 croce.
Conoscendo esattamente le probabilità dove ci conviene scommettere? Ovviamente il buon senso ci dice su croce e si dimostra abbastanza facilmente perché. Su 100 lanci vinceremo
circa 50 volte. Puntando ancora una volta 1 euro avremo un guadagno netto di 55 euro contando tutte le volte che esce croce e 50 euro di perdite sommando tutte le volte che esce testa. Quindi avremo fatto un utile di 5 euro. In caso contrario avremo una perdita di 5 euro.
Consideriamo, adesso, un caso controintuitivo. Immaginiamo di considerare una moneta truccata. Questa moneta ha lo 0.8 di probabilità di mostrarci una testa e 0.2 di probabilità di mostrarci una croce. Se la testa viene pagata a 1.2 e la croce viene pagata a a 5.1 su chi conviene scommettere? Facciamo i conti.
Una probabilità di 0.8 significa che su 100 lanci avremo circa 80 teste e 20 croci. Se puntiamo sulla testa (sempre 1 euro, non siamo Briatore) avremo una guadagno netto di 96-100=-4 euro, dove 96 è dato 80*1.2 e 100 è il denaro complessivo investito in 100 lanci. Cioè avremo perso 4 euro. Se invece puntiamo su croce avremo un guadagno netto 102-100=2 euro. Cioè sul lungo periodo è più conveniente puntare sulla croce anche se vince molte meno volte.
Quindi, estrapolando questo concetto, ai fini di un giocatore d'azzardo è inutile sapere che il Barcellona è la squadra di calcio più forte del mondo, bisogna sapere quanto è più forte delle altre e questo per poter valutare se sia conveniente scommettere a favore o contro. Estrapolando ancora, si vede immediatamente che giochi come il lotto, sono sfavorevoli allo scommettitore, perchè sul lungo periodo pagano meno del denaro complessivo investito.
Le scommesse a montepremi sono un po' più complicate e vedremo più in la perché.
La regola generale per sapere se una scommessa a quota fissa è favorevole o meno è data da p(a)*Q(a)=k(a), dove p(a) è la probabilità di verificarsi di a,
Q(a) è la quota e k(a) è la bontà della scommessa. Se k(a)>1 la scommessa è favorevole a chi punta. Se k(a)=1 è una fair bet, se k(a)<1 la scommessa è sfavorevole. Adesso si capisce anche perché le quote decimali sono le più comode da usare. Come possiamo formalizzare questo concetto? Immaginiamo di che il nostro capitale sia V0, che la nostra quota sia Q(a) e che la probabilità che si verifichi l'evento a sia P(a). Immaginiamo ora di investire una frazione f del nostro capitale V0 in questa scommessa. In caso di vittoria avremo al passo 1 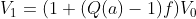
ovvero il nostro capitale viene incrementato di una quantità (Q(a)-1)f V_0. In caso di sconfitta avremo che il nostro capitale al passo 1 sarà
Immaginiamo che la la nostra scommessa possa essere giocata N volte alle stesse condizioni. Allora avremo che in generale al passo N il nostro capitale sarà
dove W è il numero di volte che abbiamo vinto e L è il numero di volte che abbiamo perso. Se la probabilità dell'evento è p(a) avremo che in media W=p(a)N
mentre L=(1-p(a))N=q(a)N, allora possiamo scrivere
quindi possiamo immaginare che ad ogni scommessa ci sarà una variazione di capitale
allora la frazione di capitale da scommettere sarà quella che massimizza il guadagno medio
Questa si calcola facilmente applicando il logaritmo naturale ad ambo i lati derivando e imponendo che si auguale a 0. Quindi abbiamo
il risultato è
Questa è la famosa formula di Kelly e la massimizzazione del guadagno sul lungo periodo si chiama criterio di Kelly. Se f>0 allora la scommessa è vantaggiosa e bisogna comprare, se f=0 è una fair bet, se f<0 è svantaggiosa per chi punta, ma è vantaggiosa per chi vende. Quindi quando possibile bisogna vendere a quella quota quella determinata scommessa. E.g. se f=0.2 significa che bisogna investire lo 0.2 ( cioè il 20%) del nostro capitale in quella scommessa. Se fosse stato -0.2 avremmo dovuto vendere il 20% del nostro capitale a quella quota. Esiste, tuttavia, una ragione molto buona per non puntare mai la quota esatta di kelly. Infatti come detto le probabilità devono essere considerate come vere e proprio quantità fisiche e quindi non sono mai conosciute con esattezza (a parte rari casi) e quindi è sempre preferibile puntare una frazione del valore di Kelly. Il perché è abbastanza intuitivo: puntare troppo forte aumenta enormemente le nostre possibilità di rovina. E.g. consideriamo ancora una volta l'esempio della moneta truccata. Puntare tutto ad ogni colpo su testa è la maniera più rapida in assoluto per perdere tutto. Questo si può vedere anche matematicamente. Per f troppo grandi il guadango medio G(f) diventa negativo. Tecnicamente vendere una scommesa si dice bancare o laying (puntare si definisce anche backing) e al momento in Italia è vietato. Esiste, alla luce di quanto detto fino adesso, una maniera di simulare una bancata con sole puntate? Vediamo cosa ci dice il criterio di Kelly. Consideriamo il caso semplice di una semplice scommessa di calcio sul 1,x,2. De finiamo p(1),p(x) e p(2) le rispettive probabilità dei risultati. Q(1),Q(x) e Q(2) le quote. Immaginiamo adesso che il criterio di Kelly ci abbia appena fatto sapere che scommettere sul 2 è svantaggioso. Come dovremmo ripartire le puntate f1 e fx (frazine sull'1 e frazione sull'x) sul 1 e sul x? Seguendo il criterio di kelly abbiamo 3 casi possibili. Il primo caso è che esca l'1, quindi considerando solo questo avremo un incremento medio 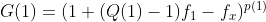
se esce l'x, cioè il secondo caso, avremo
e se esce il 2 (terzo caso) avremo
Quindi nel caso generale avremo
Allora secondo il criterio di Kelly è necessario massimizzare la quantità G rispetto a f1 e fx. La soluzione è piuttosto semplice ed è
dove a=Q(1)-1 e b=Q(x)-1. Quindi generalizzando per calcolare un caso generico seondo il criterio di Kelly, bisogna calcolare tutti casi possibili e poi massimizzarne il prodotto.
Ok anche per questo post credo che sia abbastanza a presto :)
Referenze:
Kelly, J.L. Jr. "A New Interpretation of Information Rate," Bell Systems Technical Journal, 35, (1956), 917-926 [pdf format; 101k]
Referenze:
Kelly, J.L. Jr. "A New Interpretation of Information Rate," Bell Systems Technical Journal, 35, (1956), 917-926 [pdf format; 101k]